Spatial Modeling | Elston Lab

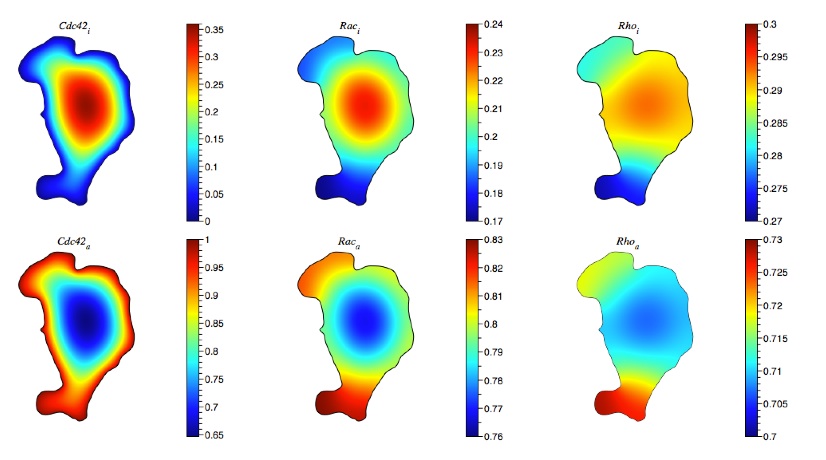
Another focus of our laboratory is to understand the spatial dynamics of signaling molecules, and how this spatial distribution regulates further signal transduction in pathways. In general, molecules inside a cell have their own spatial distributions. Some proteins accumulate at specific sites near the cell membrane when they are active, some adopt uniform distributions in the cytosol. Therefore, interesting questions about the spatial dynamics of signaling molecules come about: How does a spatial distribution of a specific molecule evolve? How does signaling depend on the spatial distribution of upstream elements? What is the role of multiple feedback and feedforward loops? How does the geometry of the cell affect the finial distribution of signaling proteins?

We are interested in characterizing signaling architectures that can form precisely organized structures. We used phagosynapse formation in FcgR-mediated frustrated phagocytosis as a model experimental setup, in which an F-actin ring forms around a IgG patch printed onto a coverslip. To identify signaling motifs compatible with this behavior, we applied an evolutionary algorithm to generate ensembles of reaction-diffusion PDEs capable of mimicking the F-actin ring on a circular domain. Shown are a variety of ring-forming systems. Applying constraints based on experimentally-observed ring formation dynamics, or the distributions of other molecular species, will allow us to refine our system of models, and characterize signaling motifs consistent with phagosynapse formation.

A cut cell method for simulating spatial models

Cells use signaling networks consisting of multiple interacting proteins to respond to changes in their environment. In many situations, such as chemotaxis, spatial and temporal information must be transmitted through the network. Recent computational studies have emphasized the importance of cellular geometry in signal transduction, but have been limited in their ability to accurately represent complex cell morphologies. We present a finite volume method that addresses this problem. Our method uses Cartesian cut cells and is second order in space and time. We use our method to simulate several models of signaling systems in realistic cell morphologies obtained from live cell images and examine the effects of geometry on signal transduction.